Laplace Transform

The Laplace transform is a fundamental tool in the analysis of linear time-invariant (LTI) systems, such as electrical circuits and mechanical systems. By transforming a time-domain function \(f(t)\) into a complex frequency-domain representation \(F(s)\), it provides a convenient method to study the behavior of systems using algebraic techniques. One of the main benefits of the Laplace transform is that it converts complex differential equations into simple algebraic equations, making it much easier to solve them and interpret system dynamics.

Definition 13

Laplace Transform: The Laplace transform is an integral transform used to convert a time-domain function \(f(t)\) into a complex frequency-domain representation \(F(s)\). It is defined as:

\[ F(s) = \mathcal{L}\{f(t)\} = \int_0^{\infty} f(t) e^{-st} \, dt, \quad s \in \mathbb{C} \]

where:

• \(f(t)\) is the time-domain function,

• \(s\) is a complex variable defined as \(s = \sigma + j\omega\),

• \(e^{-st}\) is the kernel of the transform,

• \(\mathcal{L}\{\cdot\}\) denotes the Laplace transform operator.

This transformation is useful for analyzing linear time-invariant (LTI) systems, solving differential equations, and understanding system dynamics in the frequency domain.

Properties of the Laplace Transform

The Laplace transform has several key properties that make it a versatile tool in mathematics and engineering. Understanding these properties is essential for solving differential equations and system analysis.

Theorem 5

Linearity of the Laplace Transform: If \(a\) and \(b\) are constants, and \(f(t)\) and \(g(t)\) are time-domain functions, then the Laplace transform of a linear combination is given by:

\[ \mathcal{L}\{a f(t) + b g(t)\} = a \mathcal{L}\{f(t)\} + b \mathcal{L}\{g(t)\} \]

This property implies that the Laplace transform of a sum of scaled functions is the same as the sum of their individual Laplace transforms, each scaled accordingly.

The linearity property is useful for breaking down complex functions into simpler components and analyzing each part separately. It also simplifies solving ordinary differential equations (ODEs), as it allows us to consider individual terms independently.

→ The Laplace transform effectively transforms differential equations into algebraic equations, simplifying the process of solving complex systems.

Another important property of the Laplace transform is its ability to shift functions in the time domain, which can be critical when dealing with delayed or advanced signals.

Theorem 6

First Shifting Theorem: If \(\mathcal{L}\{f(t)\} = F(s)\), then the Laplace transform of \(e^{at} f(t)\) is given by:

\[ \mathcal{L}\{e^{at} f(t)\} = F(s-a) \]

This theorem is particularly useful for incorporating exponential terms and understanding how a shift in the time domain affects the frequency domain representation.

This property helps analyze signals that grow or decay exponentially over time. For example, applying this theorem allows us to directly compute the Laplace transform of functions multiplied by \(e^{at}\), rather than redoing the entire integration.

→ When using the Laplace transform, initial conditions (values of \(f(t)\) and its derivatives at \(t=0\)) play a significant role in determining the solution to differential equations.

This emphasis on initial conditions highlights another advantage of using the Laplace transform: it inherently incorporates the initial state of a system, making it easier to solve initial value problems in ODEs.

Example: Inverse Laplace Transform Using Partial Fractions

To better illustrate the practical application of the Laplace transform, let’s consider an example where we find the inverse Laplace transform of a given function using partial fraction decomposition. Suppose we have:

\[ V(s) = \frac{10s^2 + 4}{s(s+1)(s+2)^2} \]

Our goal is to find \(v(t)\) by using the inverse Laplace transform. The process involves expressing \(V(s)\) as a sum of simpler fractions, each of which can be easily transformed back into the time domain. Let’s see how this can be done step-by-step:

1. Decompose into Partial Fractions:

We start by expressing \(V(s)\) in terms of simpler fractions:

\[ \frac{10s^2 + 4}{s(s+1)(s+2)^2} = \frac{A}{s} + \frac{B}{s+1} + \frac{C}{s+2} + \frac{D}{(s+2)^2} \]

2. Solve for Constants:

Multiply through by the common denominator \(s(s+1)(s+2)^2\) and equate coefficients:

\[ 10s^2 + 4 = A(s+1)(s+2)^2 + B s(s+2)^2 + C s(s+1)(s+2) + D s(s+1) \]

By expanding and matching coefficients for different powers of \(s\), we find:

• \(A = 2\)

• \(B = 4\)

• \(C = -2\)

• \(D = 0\)

3. Rewrite the Fraction:

Now we can write:

\[ V(s) = \frac{2}{s} + \frac{4}{s+1} - \frac{2}{s+2} \]

4. Inverse Laplace Transform:

Using standard Laplace transform pairs:

• \(\mathcal{L}^{-1}\left\{\frac{2}{s}\right\} = 2\)

• \(\mathcal{L}^{-1}\left\{\frac{4}{s+1}\right\} = 4 e^{-t}\)

• \(\mathcal{L}^{-1}\left\{\frac{-2}{s+2}\right\} = -2 e^{-2t}\)

5. Final Solution:

The time-domain function \(v(t)\) is:

\[ v(t) = 2 + 4 e^{-t} - 2 e^{-2t} \]

This example demonstrates how partial fraction decomposition can simplify the inverse Laplace transform process, making it straightforward to retrieve the original time-domain function.

The ability to transform complex functions into simpler ones is what makes the Laplace transform a powerful tool in both mathematical and engineering applications.

Table of Laplace Transform Properties

Property	Time-Domain Expression	Laplace Transform	Explanation
Linearity	\(a f(t) + b g(t)\)	\(a F(s) + b G(s)\)	The transform of a linear combination is the same as the linear combination of their transforms.
Differentiation in Time	\(f'(t)\)	\(s F(s) - f(0)\)	Transforms a derivative into an algebraic expression.
Differentiation in Frequency	\(t f(t)\)	\(- \frac{dF(s)}{ds}\)	Multiplying by \(t\) in the time domain differentiates the transform in the \(s\)-domain.
Integration in Time	\(\int_0^t f(\tau) d\tau\)	\(\frac{F(s)}{s}\)	Integrating a function results in division by \(s\) in the \(s\)-domain.
Integration in Frequency	\(\frac{f(t)}{t}\)	\(\int_s^\infty F(\sigma) d\sigma\)	Division by \(t\) in the time domain results in integration in the \(s\)-domain.
Time Shifting	\(f(t - a) u(t - a)\)	\(e^{-as} F(s)\)	Delaying a function by \(a\) seconds multiplies its transform by \(e^{-as}\).
Frequency Shifting	\(e^{at} f(t)\)	\(F(s - a)\)	Exponential multiplication shifts the frequency domain by \(a\).
Scaling in Time	\(f(at)\)	$\frac{1}{	a
Initial Value Theorem	\(\lim_{t \to 0^+} f(t)\)	\(\lim_{s \to \infty} s F(s)\)	Provides the initial value of the function without needing the inverse transform.
Final Value Theorem	\(\lim_{t \to \infty} f(t)\)	\(\lim_{s \to 0} s F(s)\)	Yields the final value of the function directly from the Laplace transform.
Convolution	\((f * g)(t) = \int_0^t f(\tau) g(t - \tau) d\tau\)	\(F(s) G(s)\)	Convolution in time corresponds to multiplication in the frequency domain.
Multiplication by \(t^n\)	\(t^n f(t)\)	\((-1)^n \frac{d^n F(s)}{ds^n}\)	Multiplying by \(t^n\) corresponds to the \(n^{th}\) derivative in the frequency domain.
Complex Conjugation	\(f^*(t)\)	\(F^*(-s^*)\)	The conjugate of a time-domain function results in conjugating and flipping the frequency domain.
Real Part	\(\text{Re}\{f(t)\}\)	\(\frac{F(s) + F^*(s^*)}{2}\)	The real part of \(f(t)\) can be extracted using the average of the transform and its conjugate.
Imaginary Part	\(\text{Im}\{f(t)\}\)	\(\frac{F(s) - F^*(s^*)}{2j}\)	The imaginary part can be retrieved using the difference of the transform and its conjugate.
Even and Odd Components	\(f_{even}(t)\), \(f_{odd}(t)\)	\(\frac{F(s) + F(-s)}{2}\), \(\frac{F(s) - F(-s)}{2}\)	Even and odd components have distinct transforms that can be separated using symmetry properties.
Laplace Transform of a Periodic Function	\(f(t) = f(t + T)\)	\(\frac{1}{1 - e^{-sT}} \int_0^T f(t) e^{-st} dt\)	For periodic functions with period \(T\), the transform simplifies using a geometric series approach.

Laplace Transform Pairs

Time Domain Function \(f(t)\)	Laplace Transform \(F(s)\)	Description	Remarks
\(1\)	\(\frac{1}{s}\)	Step Function	Basic response; \(f(t) = 1\) for \(t \geq 0\).
\(t^n \, (n \in \mathbb{N})\)	\(\frac{n!}{s^{n+1}}\)	Polynomial Function	Captures polynomial growth.
\(e^{at}\)	\(\frac{1}{s - a}\)	Exponential Growth/Decay	When \(a < 0\), indicates decay; \(a > 0\) shows growth.
\(\sin(\omega t)\)	\(\frac{\omega}{s^2 + \omega^2}\)	Sine Function	Pure oscillation with frequency \(\omega\).
\(\cos(\omega t)\)	\(\frac{s}{s^2 + \omega^2}\)	Cosine Function	Another periodic function.
\(e^{at} \sin(\omega t)\)	\(\frac{\omega}{(s - a)^2 + \omega^2}\)	Damped Sine Function	Exponential decay combined with oscillation.
\(e^{at} \cos(\omega t)\)	\(\frac{s - a}{(s - a)^2 + \omega^2}\)	Damped Cosine Function	Similar to above, but with a cosine base.
\(\delta(t)\) (Dirac Delta)	\(1\)	Impulse Function	Idealized unit impulse function at \(t = 0\).
\(u(t)\) (Unit Step)	\(\frac{1}{s}\)	Heaviside Step Function	Starts from \(0\) and jumps to \(1\) at \(t=0\).
\(t e^{at}\)	\(\frac{1}{(s-a)^2}\)	Linearly Growing Exponential	Common in control theory for ramp responses.
\(\frac{1}{\sqrt{t}}\)	\(\sqrt{\frac{\pi}{s}}\)	Inverse Square Root	Represents power law decay.
\(t^2 e^{at}\)	\(\frac{2}{(s-a)^3}\)	Quadratically Growing Exponential	Shows acceleration over time.
\(\sinh(\omega t)\)	\(\frac{\omega}{s^2 - \omega^2}\)	Hyperbolic Sine	Non-periodic, grows exponentially.
\(\cosh(\omega t)\)	\(\frac{s}{s^2 - \omega^2}\)	Hyperbolic Cosine	Similar to \(\sinh\) but symmetric.
\(t e^{-at} \sin(\omega t)\)	\(\frac{2 \omega (s-a)}{((s-a)^2 + \omega^2)^2}\)	Damped, Time-Weighted Sine	Useful for underdamped oscillatory systems.
\(t e^{-at} \cos(\omega t)\)	\(\frac{(s-a)^2 - \omega^2}{((s-a)^2 + \omega^2)^2}\)	Damped, Time-Weighted Cosine	Exhibits the combination of growth and oscillation.

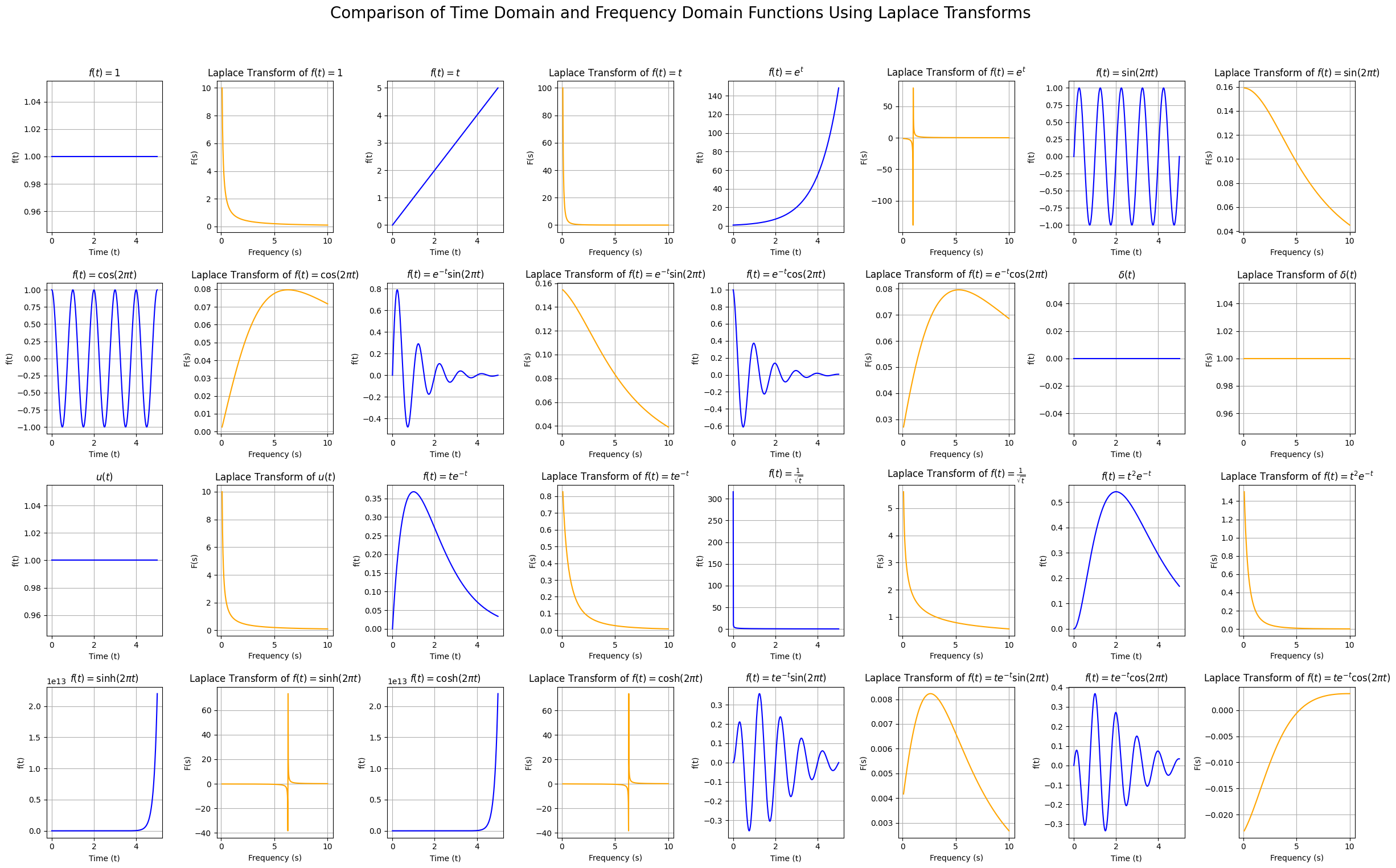
Let’s see visually how the Laplace transform pairs work

import numpy as np
import matplotlib.pyplot as plt

# Define time and s (frequency) variables
t = np.linspace(0, 5, 500)
s = np.linspace(0.1, 10, 500)

# Define each function in time domain and their corresponding Laplace transform
time_functions = [
    np.ones_like(t),                            # 1
    t,                                          # t^1
    np.exp(t),                                   # e^(t)
    np.sin(2 * np.pi * t),                       # sin(2*pi*t)
    np.cos(2 * np.pi * t),                       # cos(2*pi*t)
    np.exp(-t) * np.sin(2 * np.pi * t),          # e^(-t) * sin(2*pi*t)
    np.exp(-t) * np.cos(2 * np.pi * t),          # e^(-t) * cos(2*pi*t)
    np.zeros_like(t),                            # Delta function (approx zero)
    np.heaviside(t, 1),                          # Unit step function
    t * np.exp(-t),                              # t * e^(-t)
    1 / np.sqrt(t + 1e-5),                       # 1/sqrt(t) (avoid division by zero)
    t**2 * np.exp(-t),                           # t^2 * e^(-t)
    np.sinh(2 * np.pi * t),                      # sinh(2*pi*t)
    np.cosh(2 * np.pi * t),                      # cosh(2*pi*t)
    t * np.exp(-t) * np.sin(2 * np.pi * t),       # t * e^(-t) * sin(2*pi*t)
    t * np.exp(-t) * np.cos(2 * np.pi * t)        # t * e^(-t) * cos(2*pi*t)
]

# Define the corresponding Laplace Transforms in the frequency domain
frequency_functions = [
    1 / s,                                       # 1/s
    1 / s**2,                                    # 1/s^2
    1 / (s - 1),                                 # 1/(s-1)
    2 * np.pi / (s**2 + (2 * np.pi)**2),          # omega/(s^2 + omega^2)
    s / (s**2 + (2 * np.pi)**2),                  # s/(s^2 + omega^2)
    2 * np.pi / ((s + 1)**2 + (2 * np.pi)**2),    # omega/((s+1)^2 + omega^2)
    (s + 1) / ((s + 1)**2 + (2 * np.pi)**2),      # (s+a)/((s+a)^2 + omega^2)
    np.ones_like(s),                              # Impulse has constant Laplace transform 1
    1 / s,                                        # Unit step
    1 / (s + 1)**2,                               # 1/(s + a)^2
    np.sqrt(np.pi / s),                           # sqrt(pi/s)
    2 / (s + 1)**3,                               # 2/(s+a)^3
    2 * np.pi / (s**2 - (2 * np.pi)**2),           # omega/(s^2 - omega^2)
    s / (s**2 - (2 * np.pi)**2),                   # s/(s^2 - omega^2)
    2 * np.pi * (s + 1) / (((s + 1)**2 + (2 * np.pi)**2)**2),  # 2*omega(s+a)/(((s+a)^2 + omega^2)^2)
    ((s + 1)**2 - (2 * np.pi)**2) / (((s + 1)**2 + (2 * np.pi)**2)**2)  # ((s+a)^2 - omega^2)/(((s+a)^2 + omega^2)^2)
]

# Create a 4x4 grid for Time Domain and another for Frequency Domain plots
fig, axs = plt.subplots(4, 8, figsize=(24, 16))  # Create a larger grid to fit both plots side by side

# Titles for each plot
titles = [
    r'$f(t) = 1$', r'$f(t) = t$', r'$f(t) = e^t$', r'$f(t) = \sin(2\pi t)$',
    r'$f(t) = \cos(2\pi t)$', r'$f(t) = e^{-t} \sin(2\pi t)$', r'$f(t) = e^{-t} \cos(2\pi t)$', r'$\delta(t)$',
    r'$u(t)$', r'$f(t) = t e^{-t}$', r'$f(t) = \frac{1}{\sqrt{t}}$', r'$f(t) = t^2 e^{-t}$',
    r'$f(t) = \sinh(2\pi t)$', r'$f(t) = \cosh(2\pi t)$', r'$f(t) = t e^{-t} \sin(2\pi t)$', r'$f(t) = t e^{-t} \cos(2\pi t)$'
]

# Plot each function in the grid: Time domain on left side, Frequency domain on right side
for i in range(16):
    # Time domain plot
    axs[i // 4, 2 * (i % 4)].plot(t, time_functions[i], label='Time Domain', color='b')
    axs[i // 4, 2 * (i % 4)].set_title(titles[i])
    axs[i // 4, 2 * (i % 4)].set_xlabel('Time (t)')
    axs[i // 4, 2 * (i % 4)].set_ylabel('f(t)')
    axs[i // 4, 2 * (i % 4)].grid()
    
    # Frequency domain plot
    axs[i // 4, 2 * (i % 4) + 1].plot(s, frequency_functions[i], label='Frequency Domain', color='orange')
    axs[i // 4, 2 * (i % 4) + 1].set_title(f'Laplace Transform of {titles[i]}')
    axs[i // 4, 2 * (i % 4) + 1].set_xlabel('Frequency (s)')
    axs[i // 4, 2 * (i % 4) + 1].set_ylabel('F(s)')
    axs[i // 4, 2 * (i % 4) + 1].grid()

plt.suptitle('Comparison of Time Domain and Frequency Domain Functions Using Laplace Transforms', fontsize=20)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()