Fourier Transform of Periodic Functions

Introduction

The Fourier Transform is widely used to analyze periodic functions. A periodic function repeats itself after a fixed interval \(T\), known as the period of the function. Such functions can be represented as a sum of sinusoids with discrete frequencies, forming a Fourier series. The Fourier Transform of a periodic function, however, results in impulse-like components at specific frequencies that are harmonics of the fundamental period.

→ Key Insight: The Fourier Transform of a periodic function is not continuous but rather consists of discrete spikes, indicating energy at specific harmonic frequencies.

→ Please take a look at the following amazing tutorial on digital modulation.

1. Periodic Functions and Their Fourier Transform

A periodic function \(x(t)\) with period \(T\) satisfies:

\[ x(t) = x(t + T) \]

for all \(t\). This means that the function repeats itself every \(T\) seconds. The fundamental frequency of \(x(t)\) is defined as:

\[ f_0 = \frac{1}{T} \]

The corresponding angular frequency is \(\omega_0 = 2\pi f_0\). A periodic function can be decomposed into a Fourier series, which represents the function as a weighted sum of harmonics of the fundamental frequency.

Definition 12

The Fourier series of a periodic function \(x(t)\) with period \(T\) is given by:

\[ x(t) = \sum_{k=-\infty}^{\infty} c_k e^{j2\pi k f_0 t} \]

where:

• \(c_k\) are the Fourier coefficients defined as:

\[ c_k = \frac{1}{T} \int_{0}^{T} x(t) e^{-j2\pi k f_0 t} \, dt \]

• \(f_0 = \frac{1}{T}\) is the fundamental frequency.

The Fourier Transform of a periodic function is:

\[ \boxed{X(f) = \sum_{k=-\infty}^{\infty} c_k \delta(f - k f_0)} \]

→ This formula indicates that the Fourier Transform is composed of impulses at harmonics of the fundamental frequency, with strengths given by the Fourier coefficients.

2. Example: Fourier Transform of a Square Wave

Consider a square wave defined as:

\[\begin{split} x(t) = \begin{cases} 1, & 0 \leq t < \frac{T}{2} \\ -1, & \frac{T}{2} \leq t < T \end{cases} \end{split}\]

The square wave has only odd harmonics in its Fourier series expansion. The Fourier Transform will show impulses at these odd harmonic frequencies.

Theorem 2

If a function \(x(t)\) is periodic with period \(T\), its Fourier Transform consists of impulses at harmonics of the fundamental frequency \(f_0 = \frac{1}{T}\), given by:

\[ X(f) = \sum_{k=-\infty}^{\infty} c_k \delta(f - k f_0) \]

where the Fourier coefficients \(c_k\) are calculated as:

\[ c_k = \frac{1}{T} \int_{0}^{T} x(t) e^{-j2\pi k f_0 t} \, dt \]

→ For periodic functions, the Fourier Transform results in discrete impulses at harmonics of the fundamental frequency.

→ These impulses indicate where the energy is concentrated in the frequency domain.

Impulse Sampling and Its Fourier Transform

Introduction

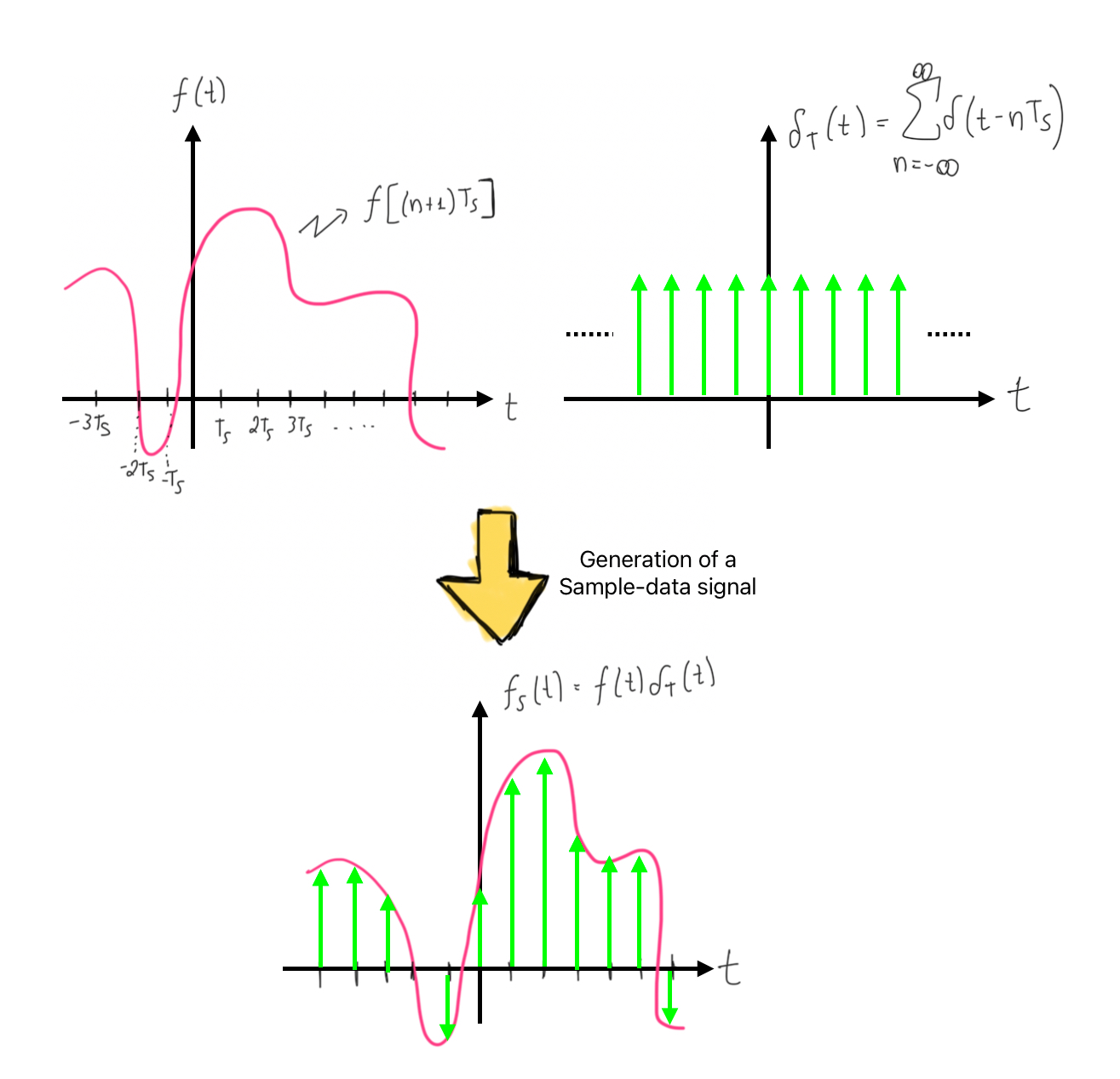
Impulse sampling is a process where a continuous-time signal is sampled using a train of impulses spaced at regular intervals. This operation is critical in understanding how signals are represented and processed in the digital domain. It allows us to move from continuous-time signals to their sampled representations, which are used in most modern communication and signal processing systems.

→ Key Insight: Impulse sampling is modeled as a modulation process in which the continuous signal is multiplied by a train of impulses, denoted by \(\delta_T(t)\).

1. Impulse Train and Sampling Operation

The impulse train is defined as a sum of Dirac delta functions spaced at intervals of \(T_s\), known as the sampling interval. Mathematically, the impulse train \(\delta_T(t)\) is given by:

\[ \delta_T(t) = \sum_{n=-\infty}^{\infty} \delta(t - nT_s) \]

where:

• \(T_s\) is the sampling period.

• \(\delta(t)\) is the Dirac delta function.

The sampling frequency is defined as:

\[ \omega_s = \frac{2\pi}{T_s} \]

Sampling frequency \(\omega_s\) indicates how often the signal is sampled in the time domain. It determines the spacing of the frequency components in the Fourier Transform of the sampled signal.

2. Modulation Process and Sampling Output

The sampling process can be represented as a modulation operation where the continuous-time signal \(f(t)\) is multiplied by the impulse train:

\[ f_s(t) = f(t) \cdot \delta_T(t) = f(t) \cdot \sum_{n=-\infty}^{\infty} \delta(t - nT_s) \]

This operation results in a sampled signal \(f_s(t)\), which is a train of weighted impulses. The value of each impulse is equal to the value of the original signal at that sampling instant.

3. Fourier Transform of the Sampled Signal

To analyze the characteristics of the sampled signal, we take the Fourier Transform of \(f_s(t)\):

\[ \mathcal{F} \{ f_s(t) \} = \mathcal{F} \left\{ f(t) \cdot \sum_{n=-\infty}^{\infty} \delta(t - nT_s) \right\} \]

Using the convolution theorem for Fourier Transforms:

Theorem 3

If \(x(t) = f(t) \cdot g(t)\), then the Fourier Transform of \(x(t)\) is:

\[ \mathcal{F} \{ x(t) \} = \frac{1}{2\pi} F(\omega) * G(\omega) \]

where \(*\) denotes convolution in the frequency domain, and \(F(\omega)\) and \(G(\omega)\) are the Fourier Transforms of \(f(t)\) and \(g(t)\), respectively.

Applying this theorem, the Fourier Transform of \(f_s(t)\) is given by:

\[ F_s(\omega) = \frac{1}{T_s} \sum_{k=-\infty}^{\infty} F(\omega - k\omega_s) \]

This equation shows that the Fourier Transform of the sampled signal \(f_s(t)\) is a replica of the original spectrum \(F(\omega)\), repeated at intervals of \(\omega_s\).

→ Aliasing: If the sampling frequency \(\omega_s\) is not high enough, the replicas overlap, causing a phenomenon known as aliasing.

The image below illustrates the modulation process of a signal.

Python Code for Visualizing Impulse Sampling

import numpy as np
import plotly.graph_objects as go

# Define the time axis
t = np.linspace(0, 2, 1000)  # Time from 0 to 2 seconds

# Create a train of square waves
square_wave_train = np.sign(np.sin(2 * np.pi * 2 * t))  # A square wave with a period of 0.5 seconds (frequency = 2 Hz)

# Define the carrier signal for modulation (fixed frequency)
carrier_frequency = 10  # Carrier frequency in Hz
carrier_signal = np.cos(2 * np.pi * carrier_frequency * t)

# Modulate the square wave using frequency modulation (FM)
initial_modulated_signal = square_wave_train * carrier_signal

# Create frames for the animation by varying the square wave frequency over time
frames = []
for freq in np.linspace(1, 5, 50):  # Vary the square wave frequency from 1 Hz to 5 Hz
    changing_square_wave = np.sign(np.sin(2 * np.pi * freq * t))  # Change the frequency of the square wave
    modulated_signal = changing_square_wave * carrier_signal  # Modulate with the same carrier signal
    frames.append(go.Frame(data=[
        # Update the square wave
        go.Scatter(x=t, y=changing_square_wave, mode='lines', name=f'Square Wave (Freq = {freq:.2f} Hz)', xaxis='x1', yaxis='y1'),
        # Update the modulated wave
        go.Scatter(x=t, y=modulated_signal, mode='lines', name=f'Modulated Signal (Freq = {freq:.2f} Hz)', xaxis='x2', yaxis='y2')
    ]))

# Create the initial plot with two subplots for side-by-side comparison
fig = go.Figure(
    data=[
        go.Scatter(x=t, y=square_wave_train, mode='lines', name='Square Wave Train', xaxis='x1', yaxis='y1'),
        go.Scatter(x=t, y=initial_modulated_signal, mode='lines', name='Modulated Signal', xaxis='x2', yaxis='y2')
    ],
    layout=go.Layout(
        title="Square Wave Train and Its Frequency Modulated Signal",
        xaxis1=dict(title='Time (s)', domain=[0, 0.45]),  # Left graph for square wave
        yaxis1=dict(title='Amplitude'),
        xaxis2=dict(title='Time (s)', domain=[0.55, 1]),  # Right graph for modulated signal
        yaxis2=dict(title='Amplitude'),
        updatemenus=[dict(type="buttons", showactive=False,
                          buttons=[dict(label="Play",
                                        method="animate",
                                        args=[None, {"frame": {"duration": 100, "redraw": True}}])])]),
    frames=frames
)

fig.show()

import numpy as np
import plotly.graph_objects as go

# Define the time axis
t = np.linspace(0, 2, 1000)  # Time from 0 to 2 seconds

# Create initial sine wave with varying amplitude and phase
initial_frequency = 1  # Start with 1 Hz
initial_signal = (1 + 0.5 * np.sin(2 * np.pi * 0.5 * t)) * np.sin(2 * np.pi * initial_frequency * t + 0.3 * np.sin(2 * np.pi * 0.2 * t))

# Define the carrier signal for modulation (fixed frequency)
carrier_frequency = 10  # Carrier frequency in Hz
carrier_signal = np.cos(2 * np.pi * carrier_frequency * t)

# Modulate the signal using amplitude modulation (AM)
initial_modulated_signal = initial_signal * carrier_signal

# Create frames for the animation by changing the frequency and varying the signal shape over time
frames = []
for freq in np.linspace(1, 10, 50):  # Vary frequency from 1 Hz to 10 Hz
    # Create a non-uniform sine wave with varying amplitude and phase over time
    changing_signal = (1 + 0.5 * np.sin(2 * np.pi * 0.5 * t)) * np.sin(2 * np.pi * freq * t + 0.3 * np.sin(2 * np.pi * 0.2 * t))
    modulated_signal = changing_signal * carrier_signal  # Modulate with the same carrier signal
    frames.append(go.Frame(data=[
        # Update the sine wave
        go.Scatter(x=t, y=changing_signal, mode='lines', name=f'Frequency = {freq:.2f} Hz', xaxis='x1', yaxis='y1'),
        # Update the modulated wave
        go.Scatter(x=t, y=modulated_signal, mode='lines', name=f'Modulated Signal (Freq = {freq:.2f} Hz)', xaxis='x2', yaxis='y2')
    ]))

# Create the initial plot with two subplots for side-by-side comparison
fig = go.Figure(
    data=[
        go.Scatter(x=t, y=initial_signal, mode='lines', name='Non-uniform Sine Wave', xaxis='x1', yaxis='y1'),
        go.Scatter(x=t, y=initial_modulated_signal, mode='lines', name='Modulated Signal', xaxis='x2', yaxis='y2')
    ],
    layout=go.Layout(
        title="Non-uniform Sine Wave and Its Modulated Signal",
        xaxis1=dict(title='Time (s)', domain=[0, 0.45]),  # Left graph for non-uniform sine wave
        yaxis1=dict(title='Amplitude'),
        xaxis2=dict(title='Time (s)', domain=[0.55, 1]),  # Right graph for modulated signal
        yaxis2=dict(title='Amplitude'),
        legend=dict(orientation='h', x=0.5, y=1.15, xanchor='center'),  # Move the legend above the plot
        updatemenus=[dict(type="buttons", showactive=False,
                          buttons=[dict(label="Play",
                                        method="animate",
                                        args=[None, {"frame": {"duration": 100, "redraw": True}}])])]),
    frames=frames
)

fig.show()